今天完成的事情：听付老师讲课，今天讲了数组、树、霍夫曼编码

数组

数组的定义

数组: 由一组名字相同､下标不同的n(n≥1)个相同数据类型的数据元素a0,a1,a2,...,an-1构成的占用一块地址连续的内存单元的有限集合

数组的处理比其它复杂的结构要简单

① 数组中各元素具有统一的类型;

② 数组元素的下标一般具有固定的上界和下界,即数组一旦被定义,它的维数和维界就不再改变｡

③数组的基本操作比较简单,除了结构的初始化和销毁之外,只有存取元素和修改元素值的操作｡

高级语言中的数组是顺序结构;此处的数组既可以是顺序的,也可以是链式结构｡

数组的顺序存储表示和实现

问题:计算机的存储结构是一维的,而数组一般是多维的,怎样存放?

解决办法:事先约定按某种次序将数组元素排成一列序列,然后将这个线性序列存入存储器中｡

行优先顺序:存储时先按行从小到大的顺序存储,在每一行中按列号从小到大存储｡

列优先顺序:存储时先按列从小到大的顺序存储,在每一列中按行号从小到大存储｡

若规定好了次序,则数组中任意一个元素的存放地址便有规律可寻,可形成地址计算公式;约定的次序不同,则计算元素地址的公式也有所不同

无论规定行优先或列优先,只要知道以下三要素便可随时求出任一元素的地址

①  始结点的存放地址(即基地址)

②  维数和每维的上､下界;

③  每个数组元素所占用的单元数 

假如:每个元素占有c个存储单元

一维数组:                                   

loc(ai)=loc(a1)+(i-1)*c

m*n的二维数组(共有m行,每行有n列)

loc(aij)=loc(a11)+[(i-1)*n+j-1]*c

三维数组R[p][m][n]:

LOC(i,j,k)= LOC(0,0,0) +(i*m*n +j*n+k) *c

N维数组的顺序存储表示

#define MAX_ARRAY_DIM   8   //假设最大维数为8  

 typedef struct{  

      ELemType *base;       //数组元素基址  

      int            dim;             //数组维数  

      int          *bound;        //数组各维长度信息保存区基址  

      int         *constants;   //数组映像函数常量的基址  

   }Array;  

矩阵的存储(二维数组)

矩阵的存储

由于矩阵是由m行n列组成,逻辑上与二维数组相同,故通常用二维数组来做矩阵的存储结构｡

矩阵的运算:

1､矩阵相加  2､矩阵相间 3､矩阵相乘 4､矩阵转置5､矩阵求逆6､写数据7､读数据

2.2矩阵的传统转置

矩阵乘法:

C=AB即

算法描述:

 1､判断矩阵B的行､列是否等于A的列､行数

 2､创建A的行数B的列数的矩阵C

 3､计算C的元素值

for(int  i=0;i<m;i++)   

     for(int j=0;j<n;j++)  

         for(int k=0;k<n;k++)  

              c[i][j]+=a[i][k]*b[k][j];

树

树这个数据结构用到了递归的概念：树的子树还是树；

度：节点的子树个数；

树的度：树中任意节点的度的最大值；

兄弟：两节点的parent相同；

层：根在第一层，以此类推；

高度：叶子节点的高度为1，根节点高度最高；

有序树：树中各个节点是有次序的；

森林：多个树组成；

树的表示法 

1.双亲表示法：每个节点存储：数据、parent在数组中的下标；

2.孩子表示法：全部节点组成一个数组，每个数组指向一个单链表，存放其孩子；如下图：

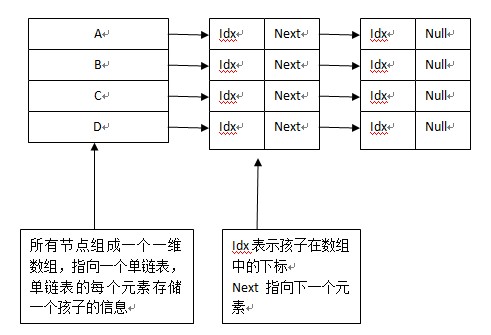
3.双亲孩子表示法

4.孩子兄弟表示法

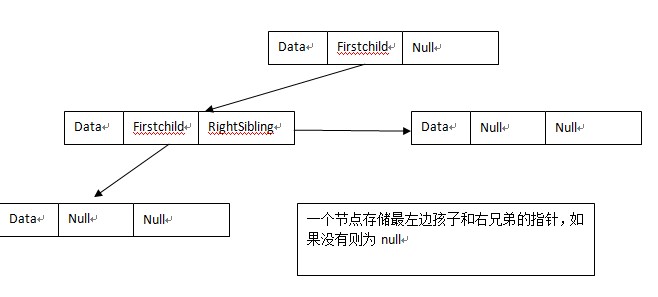
此种方法的好处在于一个多叉树能够转换成一颗二叉树，是树转换成二叉树的好办法；

线性表是树的特殊情况；

斜树：所有节点只有左节点或右节点；比如：

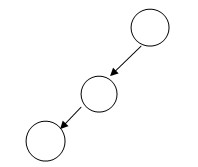
满二叉树：叶子节点一定要在最后一层，并且所有非叶子节点都存在左孩子和右孩子；

完全二叉树：从左到右、从上到下构建的二叉树；比如：

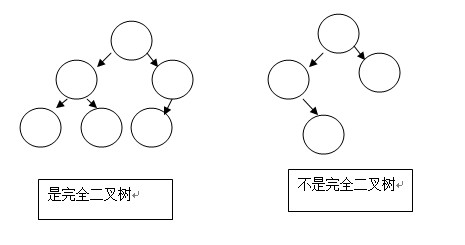
性质

1.第i层至多有2^(i-1)个节点；

2.深度为k的树最多有2^k -1个节点；

3.任意二叉树，度为0的节点数=度为2的节点数+1；

4.如果i为父亲的编号，则孩子的编号为2i和2i+1;

5.如果孩子的编号为k,则父亲的编号为floor(k/2);

二叉树的存储结构 

(1)顺序存储：只适用于完全二叉树；

(2)链式存储：最通用的存储方法；

但是这样很浪费空间，因为会有很多空指针（如果有n个节点，则有2n个left、right指针，但是用到的只有n-1个指针）

改进：线索二叉树：将空指针链接到前驱或后继节点；（此处前驱和后继是按照中序遍历上讲的）

节点数据结构如下图：

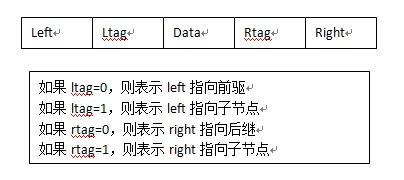
比如：

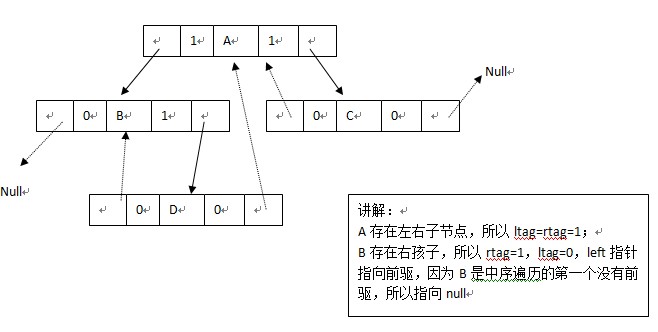
一般构造线索二叉树的过程步骤如下：

(1)构造一般二叉树；

(2)遍历二叉树的同时，建立线索二叉树；

二叉树的遍历

(1)前序遍历：先双亲、再左孩子、最后右孩子；

(2)中序遍历：先左孩子、再双亲、最后右孩子；

(3)后序遍历：先左孩子、再右孩子、最后双亲；

(4)层次遍历：一层一层，从左到右、从上到下遍历；

注意：

(1)已知前序、后序遍历结果，不能推导出一棵确定的树；

(2)已知前序、中序遍历结果，能够推导出后序遍历结果；

(3)已知后序、中序遍历结果，能够推导出前序遍历结果

扩展二叉树

对于一般二叉树的扩充，为了能够通过一个遍历序列建立二叉树，扩展二叉树如图所示：

如果存在遍历序列：AB##C##,则可以很容易的建立二叉树；

此种方式很方便，因为一般来说都需要三种遍历方式中的两种才可以确定一个二叉树；

Huffman编码

Huffman是一种前缀编码；

Huffman编码是建立在Huffman树的基础上进行的，因此为了进行Huffman编码，必须先构建Huffman树；

树的路径长度是每个叶节点到根节点的路径之和；

带权路径长度是（每个叶节点的路径长度*wi）之和；

Huffman树是最小带权路径长度的二叉树；

构造Huffman树的过程：

(1)将各个节点按照权重从小到大排序；

(2)去最小权重的两个节点，并新建一个父节点作为这两个节点的双亲，双亲节点的权重为子节点权重之和，再将此父节点放入原来的队列；

(3)重复(2)的步骤，直到队列中只有一个节点，此节点为根节点；

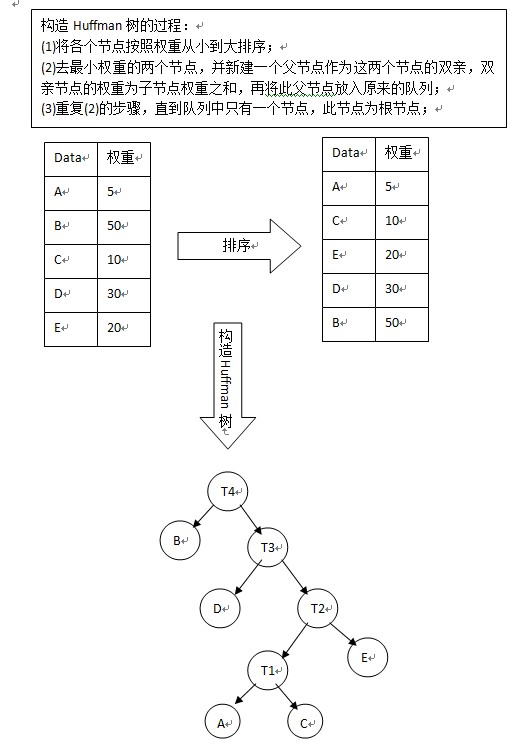
构造完Huffman树之后，就可以进行Huffman编码了，编码规则：

(1)左分支填0，右分支填1；

Huffman解码过程

(1)给定一个01串，将01串进行Huffman树，到叶子节点了就表明已经解码一个节点，然后再次遍历Huffman树；

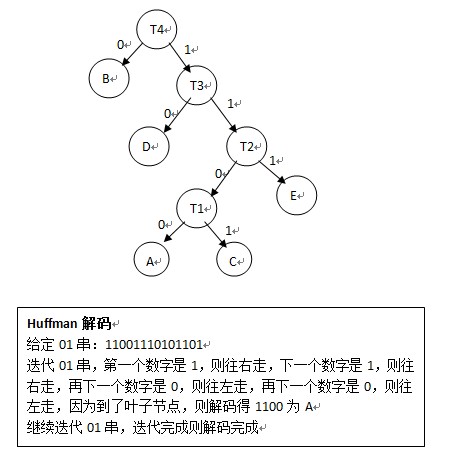
明天计划的事情:完成任务四

遇到的问题：java环境变量出了很奇怪的问题

收获：复习了一下数据结构。