发表于: 2018-09-13 22:18:11
1 931
今天完成的事情:
今天看了等价类的几个例子,改了一下测试用例
明天计划的事情:
提交任务2,几乎都总结完了就差测试用例改一下
遇到的问题:
等价类可能需要数学强才可以懂得深
收获:
等价类的设计思路:
- 根据输入条件,确定等价类,包括有效等价类和无效等价类,建立等价类列表
- 为每个等价类规定一个唯一的编号
- 设计一个测试用例,使其尽可能多地覆盖尚未被覆盖的有效等价类,重复这一步,直到所有的有效等价类被覆盖完为止
- 设计一个测试用例,使其尽可能多的覆盖尚未被覆盖的无效等价类,重复这一步,直到所有的无效等价类被覆盖完为止
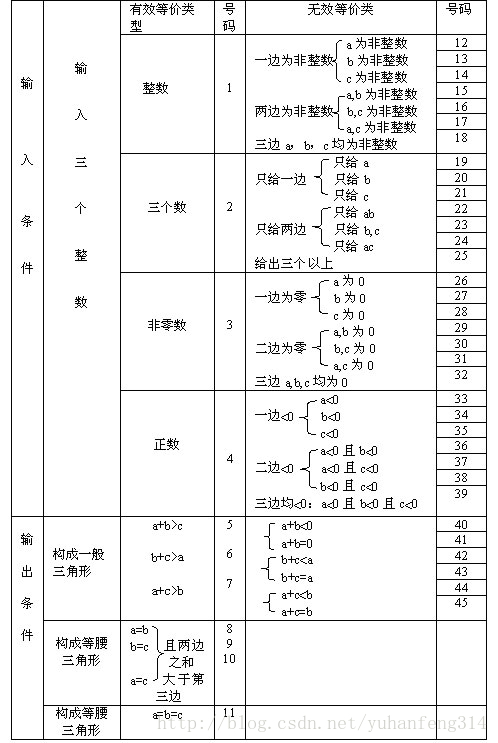
1、三角形--等价类测试的例子
某程序规定:"输入三个整数 a 、 b 、 c 分别作为三边的边长构成三角形。通过程序判定所构成的三角形的类型,当此三角形为一般三角形、等腰三角形及等边三角形时,分别作计算 … "。用等价类划分方法为该程序进行测试用例设计。(三角形问题的复杂之处在于输入与输出之间的关系比较复杂。)
分析题目中给出和隐含的对输入条件的要求:
(1)整数 (2)三个数 (3)非零数 (4)正数
(5)两边之和大于第三边 (6)等腰 (7)等边
如果 a 、 b 、 c 满足条件( 1 ) ~ ( 4 ),则输出下列四种情况之一:
1)如果不满足条件(5),则程序输出为 " 非三角形 " 。
2)如果三条边相等即满足条件(7),则程序输出为 " 等边三角形 " 。
3)如果只有两条边相等、即满足条件(6),则程序输出为 " 等腰三角形 " 。
4)如果三条边都不相等,则程序输出为 " 一般三角形 " 。
列出等价类表并编号
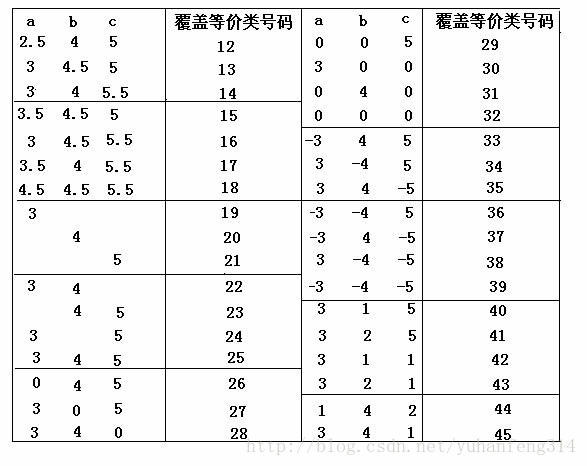
覆盖有效等价类的测试用例:
a b c 覆盖等价类号码
3 4 5 (1)--(7)
4 4 5 (1)--(7),(8)
4 5 5 (1)--(7),(9)
5 4 5 (1)--(7),(10)
4 4 4 (1)--(7),(11)
覆盖无效等价类的测试用例:
2、档案管理系统--等价类的例子
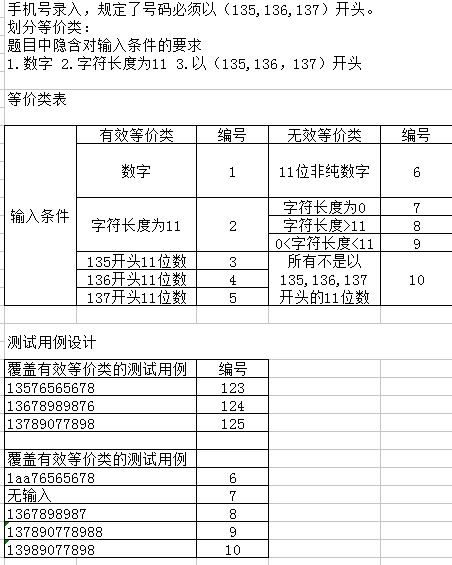
设有一个档案管理系统,要求用户输入以年月表示的日期。假设日期限定在1990年1月~2049年12月,并规定日期由6位数字字符组成,前4位表示年,后2位表示月。现用等价类划分法设计测试用例,来测试程序的"日期检查功能"。
| 输入判断 | 有效等价类 | 编号 | 无效等价类 | 编号 |
| 输入字符长度 | 6位 | ① | 大于6位数字字符 小于6位数字字符 | ⑤⑥ |
| 输入字符类型 | 数字 | ② | 6位非纯数字字符 | ⑦ |
| 输入年份约束 | 1990-2049 | ③ | 大于2049小于1990 | ⑧⑨ |
| 输入月份约束 | 01-12 | ④ | 大于12等于00 | ⑩⑾ |
3、佣金问题--等价类的例子佣金问题等价类测试用例,它是根据佣金函数的输出值域定义等价类,来改进测试用例集合。
输出销售额≤1000元 佣金10%
1000<销售额≤1800 佣金=100+(销售额-1000)*15%
销售额>1800 佣金=220+(销售额-1800)*20%
测试用例 枪机(45) 枪托(30) 枪管(25) 销售额 佣金
1 5 5 5 500 50
2 15 15 15 1500 175
3 25 25 25 2500 360
根据输出域选择输入值,使落在输出域等价类内,可以结合弱健壮测试用例结合。佣金问题分三个部分:输入数据部分,用来处理数据有效性(与三角形和档案系统管理中的一样);销售额计算;佣金计算。由于题目要求,根据佣金函数的输出值定义等价类,所以可以省略输入数据有效性部分。测试用例设计如下:
| 测试用例 | 枪机(45) | 枪托(30) | 枪管(25) | 销售额 | 佣金 | 备注 |
| 1 | 1 | 1 | 1 | 100 | 10 | 最小值 |
| 2 | 1 | 1 | 2 | 125 | 12.5 | 略大于最小值 |
| 3 | 1 | 2 | 1 | 130 | 13 | 略大于最小值 |
| 4 | 2 | 1 | 1 | 145 | 14.5 | 略大于最小值 |
| 5 | 5 | 5 | 5 | 500 | 50 | 中点 |
| 6 | 10 | 10 | 9 | 975 | 97.5 | 略小于边界值 |
| 7 | 10 | 10 | 10 | 1000 | 100 | 边界值 |
| 8 | 10 | 10 | 11 | 1025 | 103.75 | 略高于边界值 |
| 9 | 14 | 14 | 14 | 1400 | 160 | 中点 |
| 10 | 18 | 18 | 17 | 1775 | 216.25 | 略低于边界值 |
| 11 | 18 | 18 | 18 | 1800 | 220 | 边界值 |
| 12 | 18 | 18 | 19 | 1825 | 225 | 略高于边界值 |
| 13 | 48 | 48 | 48 | 4800 | 820 | 中点 |
| 14 | 69 | 80 | 90 | 7755 | 1411 | 略低于边界值 |
| 15 | 70 | 80 | 89 | 7775 | 1415 | 略低于边界值 |
| 16 | 70 | 80 | 90 | 7800 | 1420 | 输出最大值 |
此外还可以选取更接近于边界值得测试用例,比如:
| 测试用例 | 枪机 | 枪托 | 枪管 | 销售额 | 佣金 | 备注 |
| 1 | 10 | 11 | 9 | 1005 | 100.75 | 略高于边界值 |
| 2 | 18 | 17 | 19 | 1795 | 219.25 | 略低于边界值 |
| 3 | 18 | 19 | 17 | 1805 | 221 | 略高于边界值 |
4、找零问题--等价类的例子假 设 商 店 货 品 价 格 (R) 皆 不 大 於 100 元 ( 且 为 整 数 ) , 若 顾 客 付 款 在 100 元 内 (P) , 求 找 给 顾 客 之 最 少 货币 个(张) 数 ? ( 货 币 面 值 50 元 (N50) , 10 元 (N10) , 5 元 (N5) , 1 元 (N1) 四 种 ) 正确功能:找零的组合为1/10/50面值组合的最小个(张)数
找零数额=P-R 假设计算正确 一、 分 析 输 入 的 情 形 。 1.R无效: R > 100 R<=0 2.R有效: 0 < R < = 100 此种情况下再考虑P: 2_1. P无效:P > 100 (钱给多) 2_2. P无效:P < R (钱给少) 2_3. P有效:R<= P <= 100 //无效输出: 多找钱 少找钱
二、 分 析 输 出 情 形 。 考虑输出——找零个数 这里是有效数据,关于“ 找 给 顾 客 之 最 少 货币 个(张) 数”的有效取值 50:找钱面值为50元的有两种情况: 0张或/1张 10:找钱面值为10元的有五种情况: 0/1/2/3/4 5 :找钱面值为5元的有两种情况: 0/1 1 :找钱面值为1元的有五种情况:0/1/2/3/4 三、 分 析 规 格 中 每 一 决 策 点 之 情 形 考虑输出——找零数额(RR表示找零数额) 1、无效输入(不找零): R > 100 R <= 0 0 < R < = 100 P > 100 0 < R < = 100 P < R 输出为相应错误提示信息。2、有效输入(找零): 0 < R < = 100 && R<= P <= 100 此时考虑的输出:(RR=P-R 假设计算正确 不考虑此种情况无效输出) 0<=RR<5 5<=RR<10 10<=RR<50 50<=RR<100 用边界值分析法,取RR的有代表性的值,
五、为 满 足 以 上 之 各 种 情 形 , 测 试 用 例 设 计 如 下 : 1. 货品价格 = 101 无效货品价格 2. 货品价格 = 0 无效货品价格 3.货品价格 = -1 无效货品价格 4. 货品价格 = 100, 付款金额 = 101 无效付款 5. 货品价格 = 100, 付款金额 = 99 无效付款 6. 货品价格 = 100, 付款金额 = 100 不找零 7. 货品价格 = 99, 付款金额 = 100 N1=1 8. 货品价格 = 96, 付款金额 = 100 N1=4 9. 货品价格 = 95, 付款金额 = 100 N5=1 10. 货品价格 = 91, 付款金额 = 100 N5=1, N1=4 11. 货品价格 = 90, 付款金额 = 100 N10=1 12. 货品价格 = 51, 付款金额 = 100 N10=4, N5=1,N1=4 13. 货品价格 = 50, 付款金额 = 100 N50=1 14. 货品价格 = 1, 付款金额 = 100 N50=1,N10=4,N5=1,N1=4
六.





评论