今天完成的事

重新编写了下任务2的数组乱序

之前的任务2我是传了一个固定的数组过去，并没有关联玩家人数。

找了各种网站的资料，第一次尝试数组乱序是这样的，，

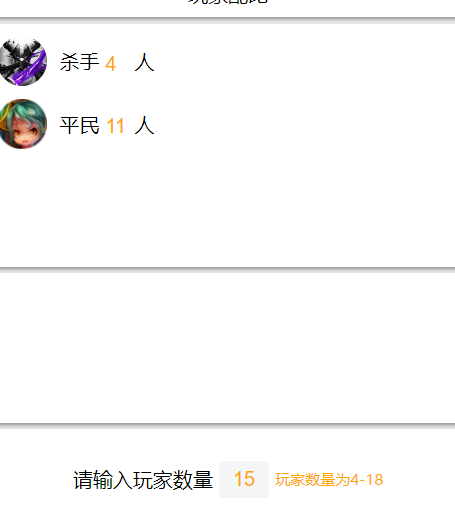
反向乱序最为致命，代入没代错，也不知道哪里出了问题。

本来以为是设置错了，将杀手跟平民输入值两个互换也不行。

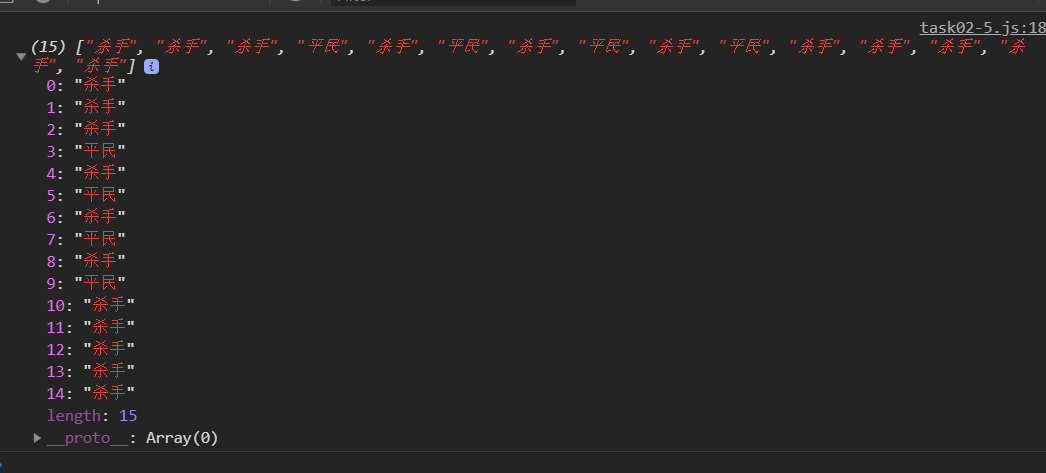
抄了另一个乱序代码之后，又能正常显示了。。

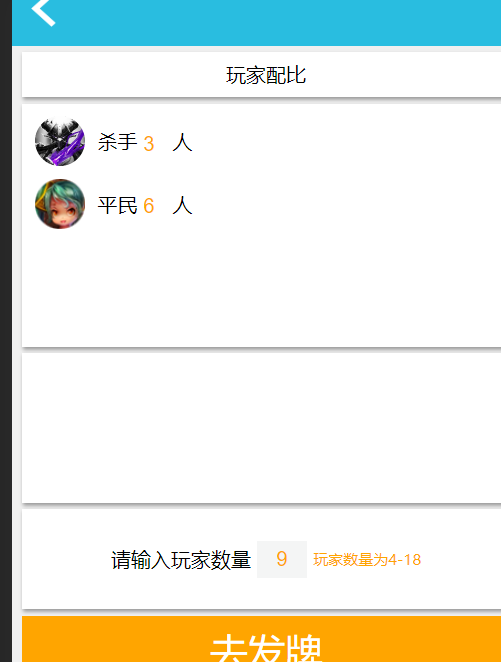
正常存入了浏览器了。

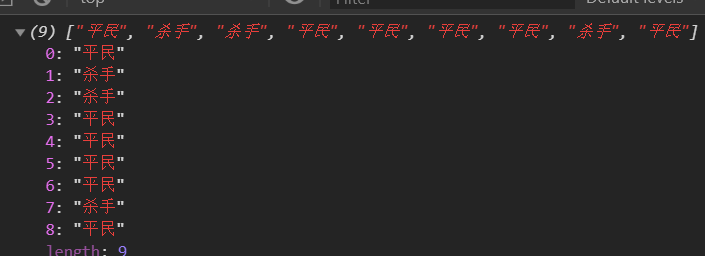
这个方法，我现在确实有些难理解

经典的随机排列

所有空间复杂度 O(1) 的排序算法的时间复杂度都介于 O(nlogn) 到 O(n²) 之间，因此在不考虑算法结果错误的前提下，使用排序来随机交换也是慢的。事实上，随机排列数组元素有经典的 O(n) 复杂度的算法：

function shuffle(arr){      var len = arr.length;      for(var i = 0; i < len - 1; i++){        var idx = Math.floor(Math.random() * (len - i));        var temp = arr[idx];
    arr[idx] = arr[len - i - 1];
        arr[len - i -1] = temp;
      }      return arr; }

在上面的算法里，我们每一次循环从前 len - i 个元素里随机一个位置，将这个元素和第 len - i 个元素进行交换，迭代直到 i = len - 1 为止。

从结果可以看出这个算法的随机结果应该是均匀的。不过我们的测试方法其实有个小小的问题，我们只测试了平均值，实际上平均值接近只是均匀分布的必要而非充分条件，平均值接近不一定就是均匀分布。不过别担心，事实上我们可以简单从数学上证明这个算法的随机性。

随机性的数学归纳法证明

对 n 个数进行随机：

1. 首先我们考虑 n = 2 的情况，根据算法，显然有 1/2 的概率两个数交换，有 1/2 的概率两个数不交换，因此对 n = 2 的情况，元素出现在每个位置的概率都是 1/2，满足随机性要求。

2. 假设有 i 个数， i >= 2 时，算法随机性符合要求，即每个数出现在 i 个位置上每个位置的概率都是 1/i。

3. 对于 i + 1 个数，按照我们的算法，在第一次循环时，每个数都有 1/(i+1) 的概率被交换到最末尾，所以每个元素出现在最末一位的概率都是 1/(i+1) 。而每个数也都有 i/(i+1) 的概率不被交换到最末尾，如果不被交换，从第二次循环开始还原成 i 个数随机，根据 2. 的假设，它们出现在 i 个位置的概率是 1/i。因此每个数出现在前 i 位任意一位的概率是 (i/(i+1)) * (1/i) = 1/(i+1)，也是 1/(i+1)。

4. 综合 1. 2. 3. 得出，对于任意 n >= 2，经过这个算法，每个元素出现在 n 个位置任意一个位置的概率都是 1/n。

参考  https://www.h5jun.com/post/array-shuffle.html

明天的计划

任务4，据说是这3个任务中最难的。。。